About
Motivation
The application of graph analysis has proven to be a useful abstraction for solving many important problems accross a variety of disciplines. In graph analysis, physical objects, abstract concepts, and other entities are represented as a set of vertices and the relationships between them are represented as edges that connect two vertices together. For example, vertices might include people, Twitter usernames, computers, cars, words, emotions, countries, events like Facebook wall posts - nearly anything. Edges might include relationships like "talks to", "lives in", "friends with", "contains", "retweets", or "posts on Facebook wall" - again, nearly any relationship. You may have noticed that the wall post example was given as both a vertex and an edge. This is because how you encode events and relationships is up to you. You could decide that these posts will be vertices and that relationships to each event might include "authored by", "commented on by", "liked by", etc. Similarly, you could decide that you would like to store a graph containing who posts on whose wall. As an trivial and somewhat frivolous example, consider the graph below consisting of the vertex types "people" and "things that are eaten" and the edge types "friends with" and "eats".
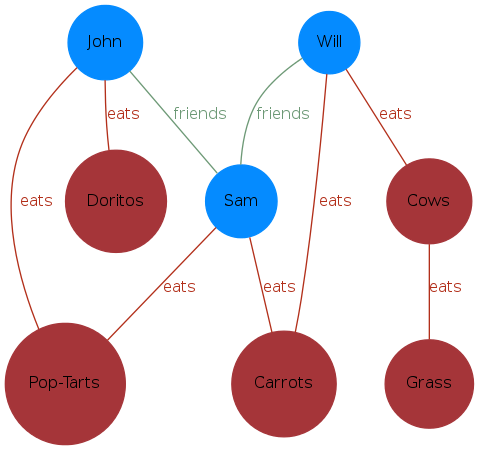
Many problems today can be formulated as dynamic spatio-temporal graph problems. For example, one may wish to track communities within social networks on Facebook as edges (friendship pairs) are added or removed. Or more interestingly, one may look for people who bridge between different social communities, or switch allegiances over time.
As the computer science community increases its development of algorithms and codes for large-scale graph problems, no canonical graph representation has yet to emerge. Without a standard graph representation, algorithms that are implemented for one framework may require substantial programming efforts to port to a different framework. Even worse, algorithms within a single framework may use different data structures for each graph kernel, requiring costly data transformations between each graph kernel subroutine. These inefficiencies in time, space, and productivity, could be reduced or eliminated through a canonical graph representation.
Objectives
- Portability: Algorithms written for STINGER can easily be translated/ported between multiple languages and frameworks. Users should be able to build and run STINGER on as many platforms as possible, and STINGER should provide support for productivity languages where possible.
- Productivity: STINGER should provide a common abstract data structure such that the large graph community can quickly leverage each others' research developments. This is similar in philosophy to the numerical algorithms community implicit use of sparse and dense matrices.
- Performance: It is recognized that no single data structure is optimal for every graph algorithm. The objective of STINGER is to configure a sensible data structure that can run most algorithms well. There should be no significant performance reduction for using STINGER when compared with another general data structure across a broad set of typical graph algorithms. STINGER should assume a shared memory address space, and allow both sequential or parallel algorithms. The data structure should allow parallel algorithms to exploit concurrency where possible.
STINGER
STINGER is a data structure for storing sparse dynamic graphs with temporal and semantic information encoded in the graph. This means that vertices in the graph have types (people, usernames, events, words, etc.) and weights, and that edges in the graph have types (friends with, sends email to, near to), weights, and timestamps (which we treat as created and modified). What the types, weights, and timestamps really mean is up to the user. As a data structure, STINGER can be extended to store more or less information with each vertex and edge as the user sees fit. A basic diagram from the original technical report defining STINGER can be seen below; however, the API for STINGER is designed to abstract away the details of the structure and simply present an interface to vertices with a set of adjacent vertices stored in edges, all having different properties that can be retrieved and set.
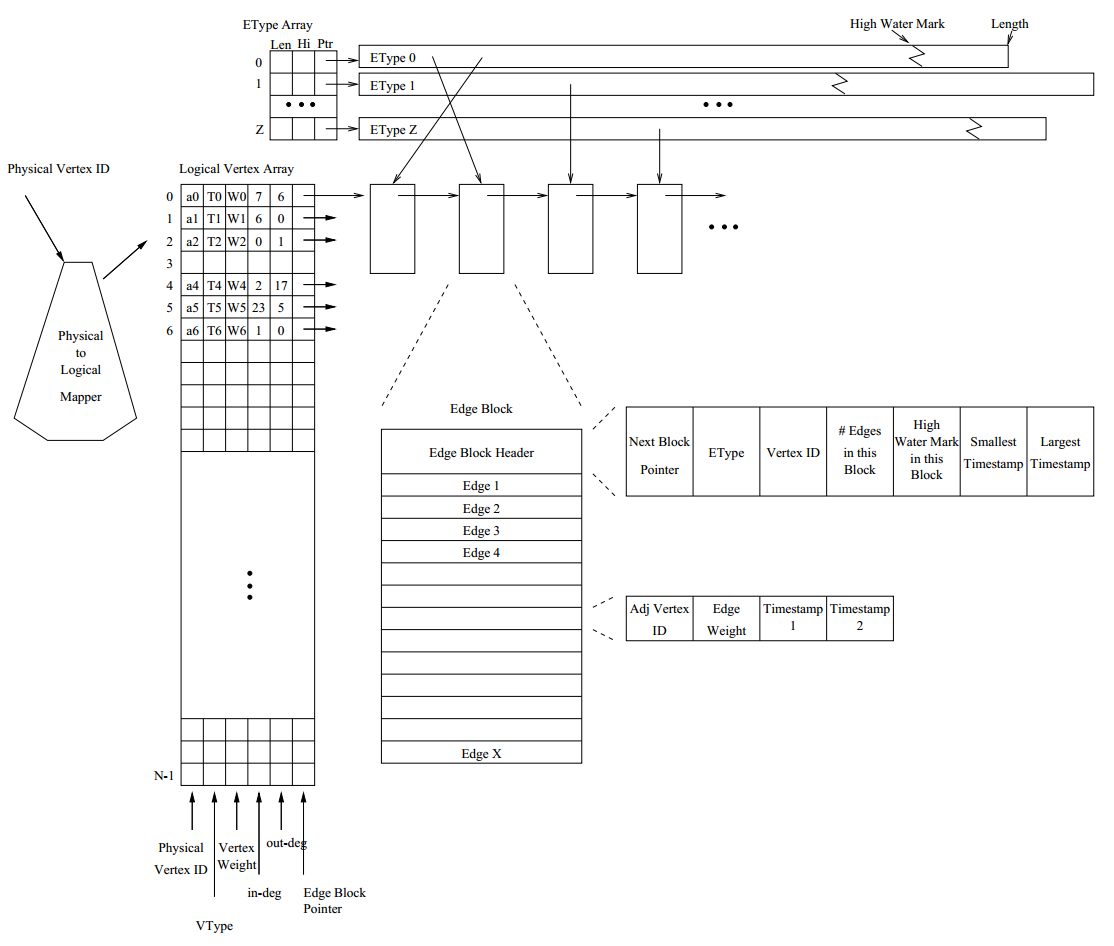
For the detail-oriented users, the data structure is similar to an adjacency list except that the adjacencies of a vertex are stored in a linked list of semi-dense blocks of edges rather than a linked list of individual edges. Also, the vertex array contains more metadata per each vertex than just a pointer to the linked of edge blocks. As you can see, vertices have physical identifiers (an arbitrary byte string that maps to that vertex), types (an arbitraty 64-bit integer value), weights (also an arbitrary 64-bit integer value), in and out degrees (set by the structure when edges are inserted and removed), and a list of adjacencies. Edge blocks contain meta data about all edges in the block including the type (so all edges in a block are of the same type).
The fact is that STINGER is also more than just this data structure. STINGER is also software and a collection of tools and algorithms that can process on these dynamic graphs to help us understand more about the data that we have.
STINGER Features
- Fast insertions, deletions, and updates:
A data structure that grows and changes at the speed of the data. - Edge and vertex types and weights:
Represent complex relationships and multiple simultaneous networks. - Filtering traversal mechanisms:
Traverse serially or in parallel on specific edge types, time ranges, vertex sets, etc. - Experimental workflow server:
Multiple data streams and analytics with one persistent data structure. - Experimental Java and Python bindings:
Use efficiency-oriented languages without sacrificing performance-oriented results.
Algorithms Implemented in STINGER
- Streaming edge insertions and deletions:
Performs new edge insertions, updates, and deletions in batches or individually. - Streaming clustering coefficients:
Tracks the local and global clustering coefficients of a graph under both edge insertions and deletions. - Streaming connected components:
Accurately tracks the connected components of a graph with insertions and deletions. - Streaming community detection:
Track and update the community structures within the graph as they change. - Parallel agglomerative clustering:
Find clusters that are optimized for a user-defined edge scoring function. - Streaming Betweenness Centrality:
Find the key points within information flows and structural vulnerabilities. - K-core Extraction:
Extract additional communities and filter noisy high-degree vertices. - Classic breadth-first search:
Performs a parallel breadth-first search of the graph starting at a given source vertex to find shortest paths.
Where to from here?
Check out the Getting Started guide for information on how to download STINGER, build it, try it out, and get started using it to power your software.
STINGER Features
- Speed: millions of updates per second on commodity hardware.
- Scale: graphs with millions to billions of vertices and edges.
- Simplicity: simple code with provided conveniences to allow developers to focus on the algorithms and data, not the data structure.
- Flexible: Full client-server framework supports multiple simultaneous ingest streams and live output to rich web visualizations
- Built for analytics
- Vertices with:
- Edges with:
- Edge Type
- Weight
- Timestamps
- Adjacent vertices of any type
- Developer-extendable attributes